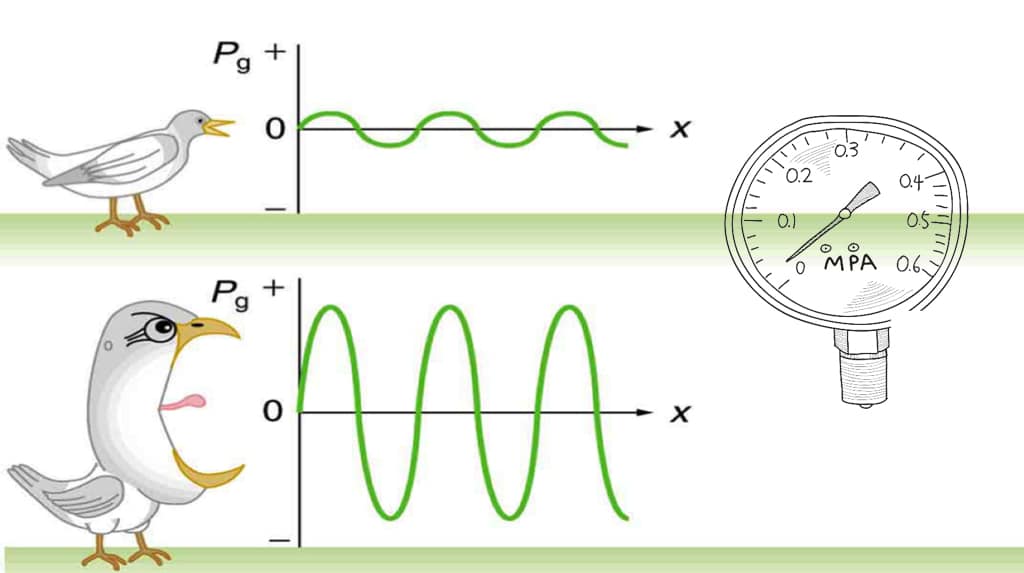
Euler’s Equation: Find the velocity of a particle (atoms, molecules in a medium that propagates sound)
Sound intensity is the product (time-averaged) of the pressure and the particle velocity
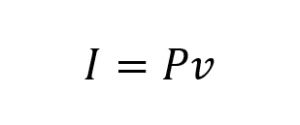
Using a microphone can measure sound pressure, but particle velocity is not so simple. However, the particle velocity can be calculated from the pressure gradient via the linear Euler equation. With this equation, we can measure the pressure gradient with two microphones close to each other and from that calculate the particle velocity.
The Euler equation is essentially the application of Newton’s second law to fluid mechanics. Newton’s second law shows the relationship between acceleration, mass, and force. If we know the force and the mass, we can calculate the acceleration. With acceleration, velocity will be calculated (integral calculus).
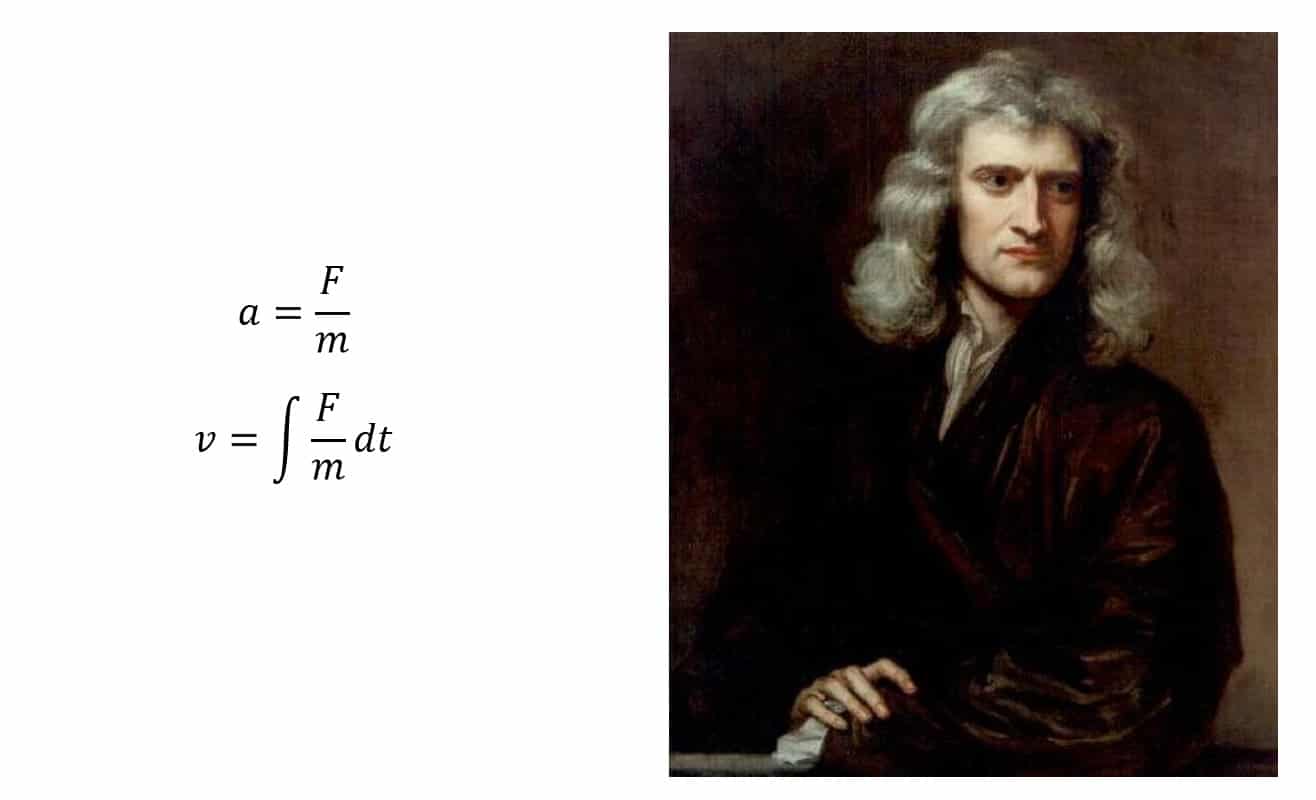
The Euler equation describes that when a pressure gradient acts on a fluid with a density of , it will cause an acceleration on the particles of that fluid as follows:

Considering the pressure gradient in one direction, we have:
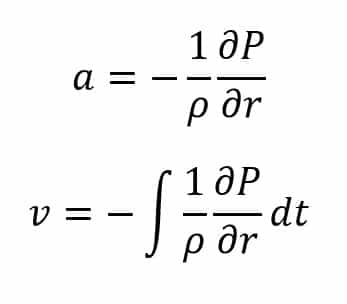
Finite approximation
The pressure gradient is a continuous function, so, with two microphones placed close together, we can treat the variation of the gradient as a straight line and use a simple approximation:
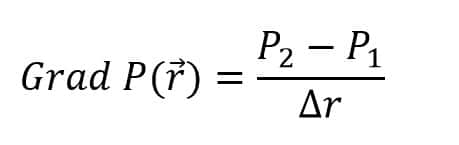
Where P1 and P2 are the measured sound pressure at the location of microphone 1 and microphone 2.
Now we will integrate the pressure gradient to get the particle velocity
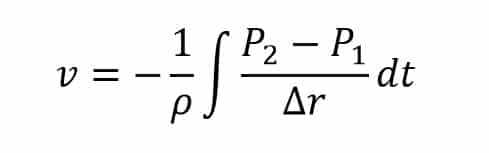
Finally, we have the sound intensity defined as follows
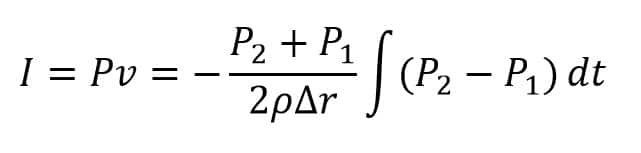
In which
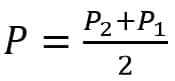
In summary, there are two ways to determine the intensity of sound.
- The first is based on the method of using Euler equations for fluid mechanics as described above.
- The second way is to calculate the imaginary part of the Cross-spectrum of the two signals received from the two microphones.
Leave a Reply